1. 정의
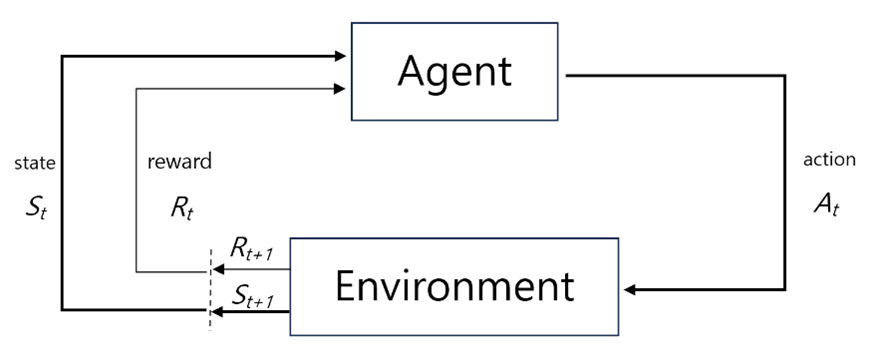
강화학습(Reinforcement Learning, RL)은 에이전트(Agent)가 환경(Environment)과 상호작용하면서 보상(Reward)을 최대화하는 행동(Policy)을 학습하는 기계학습 기법.
- 에이전트는 환경의 상태(State)를 관찰하고, 특정 행동(Action)을 선택하며, 그 결과로 보상을 받으며, 이 과정을 반복하면서 최적의 정책(Optimal Policy)을 학습
2. 핵심 기술
|
기술명
|
설명
|
|
마르코프 결정 과정(MDP)
|
상태(State), 행동(Action), 보상(Reward), 상태 전이 확률(Transition Probability), 감가율(Discount Factor)로 구성된 강화학습의 수학적 모델링 방법
|
|
정책(Policy)
|
에이전트가 특정 상태에서 어떤 행동을 선택할지를 결정하는 전략으로, 확률적 정책(Stochastic)과 결정적 정책(Deterministic)으로 구분
|
|
가치 함수(Value Function)
|
특정 상태 또는 상태-행동 쌍의 가치를 평가하는 함수로, 상태 가치 함수(V)와 행동 가치 함수(Q)로 나뉨
|
|
탐색-활용 균형
|
최적 정책을 학습하기 위해 새로운 행동을 탐색(Exploration)하는 것과 기존 학습된 지식을 활용(Exploitation)하는 것 사이의 균형 조절 방법
|
|
Q-러닝(Q-Learning)
|
환경의 모델 없이 행동 가치 함수(Q)를 학습하여 최적 정책을 도출하는 오프라인 강화학습 알고리즘
|
|
딥 Q-네트워크(DQN)
|
딥러닝을 활용하여 Q-값을 근사하는 방법으로, 높은 차원의 상태 공간에서도 효과적으로 학습 가능
|
|
정책 그래디언트(Policy Gradient)
|
정책을 직접 학습하는 기법으로, 확률적 정책을 최적화하기 위해 그래디언트 기반 학습을 사용
|
3. 강화학습의 활용 방안
|
활용 분야
|
설명
|
|
로보틱스
|
로봇의 자율 제어 및 최적의 동작 학습에 활용됨
|
|
게임 AI
|
강화학습을 통해 게임 내 인공지능이 최적의 전략을 학습함 (예: 알파고)
|
|
추천 시스템
|
사용자 행동 데이터를 기반으로 최적의 콘텐츠를 추천하는 데 활용됨
|
|
금융 및 트레이딩
|
주식 및 외환 거래에서 최적의 매매 전략을 학습하는 데 사용됨
|
|
의료 및 헬스케어
|
치료 계획 최적화 및 신약 개발을 위한 강화학습 응용 사례 존재함
|
4. 강화학습 기술 발전 방안
|
발전 방향
|
설명
|
|
효율적인 탐색 방법 연구
|
샘플 효율성을 높이고 빠른 수렴을 위한 새로운 탐색 전략 개발 필요함
|
|
일반화 능력 향상
|
특정 환경이 아닌 다양한 환경에서도 성능을 유지하는 학습 기법 연구 필요함
|
|
연산 비용 절감
|
강화학습 모델의 학습 속도 향상 및 연산 자원 효율적 활용 방안 필요함
|
|
설명 가능성 강화
|
강화학습 모델이 특정 행동을 선택한 이유를 설명할 수 있도록 하는 연구 중요함
|
"끝"
'ITPE > 인공지능_데이터분석' 카테고리의 다른 글
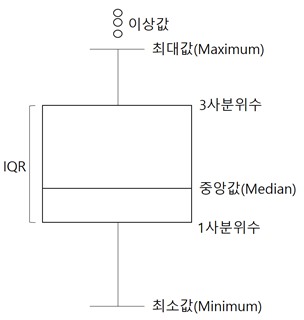
| Boxplot (0) | 2021.04.12 |
|---|---|
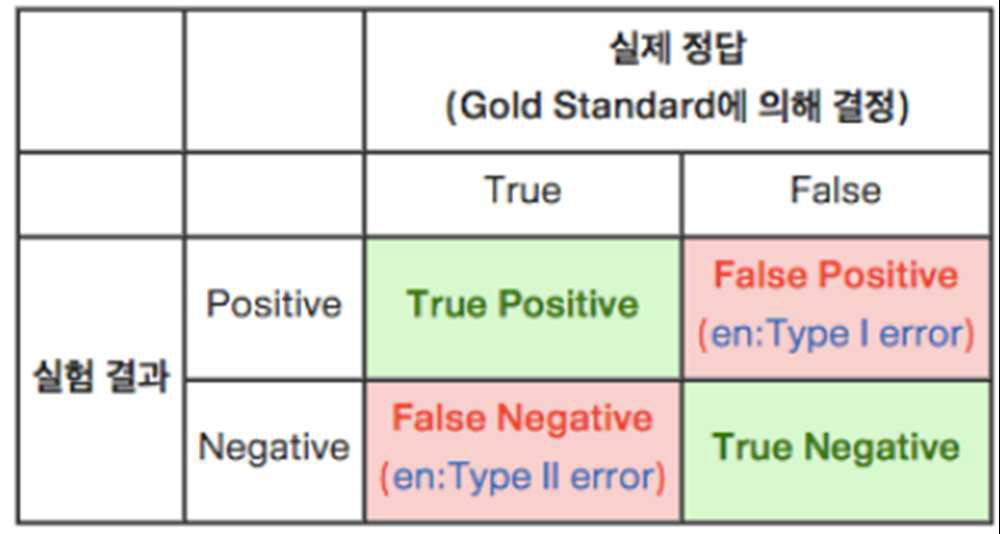
| 혼동 행렬(confusion matrix)을 이용한 분류 모형의 평가지표 (0) | 2021.04.09 |
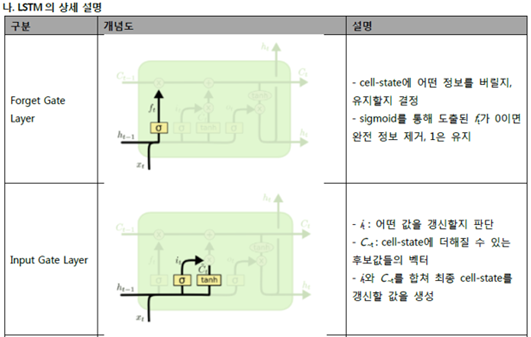
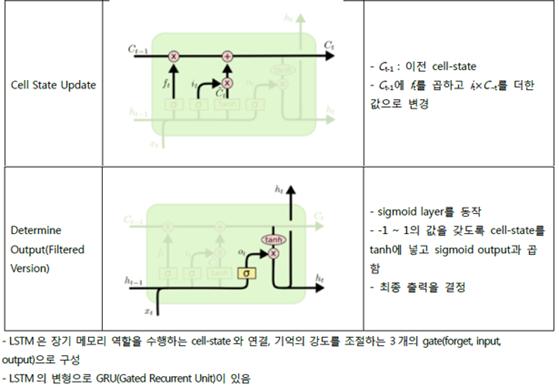
| LSTM (0) | 2021.04.09 |